Calcul de la constante magique

Un carré magique d’ordre N contient tous les entiers de 1 à N^². La somme de toutes ses cases vaut donc S = 1 + 2 + … + N^². Une formule classique dit que la somme des entiers de 1 à X vaut X(X+1)/2 (On peut s’en convaincre en groupant les termes par deux à partir du début et de la fin : 1 et X, puis 2 et X-1, puis 3 et X-2, etc. Chaque paire a pour somme X+1, et il y a X/2 paires.) La somme de toutes les cases de notre carré magique vaut donc S = N^²(N^²+1)/2.

Puisque les N lignes ont toutes la même somme (selon la définition d’un carré magique), chaque ligne a pour somme un N-ème de la somme totale du carré. La constante magique est donc S/N = N(N^²+1)/2. On retrouve les valeurs données dans l’article : pour N=3 la constante est 3×(3^²+1)/2 = 3×10/2 = 15 ; pour N = 4 elle vaut 4×(4^²+1)/2 = 4×17/2 = 34.

Nombres premiers

Voici le plus petit carré magique composé uniquement de nombres premiers.

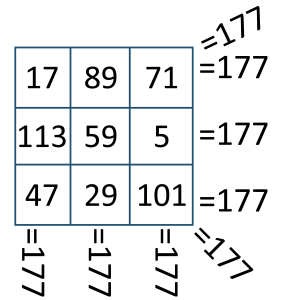
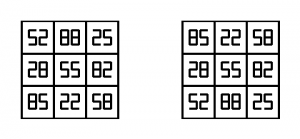
Carré magique réversible

Ce carré magique de constante 165, n’utilisant que les chiffres 2, 5 et 8, garde la même constante quand on le retourne la tête en bas.

Carré doublement alphamagique

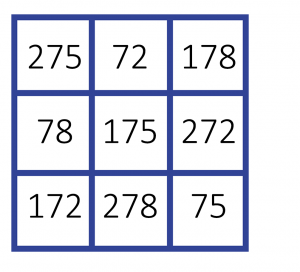
Le nom des très grands nombres en français n’étant pas parfaitement standardisé, il est utile de préciser les régles employées. Ici nous avons choisi, par souci de régularité, de ne pas utiliser le mot « milliard ». Nous dirons 106 (un 1 suivi de six 0) = un million, 109 = mille millions, 1012 = un billion, 1015 = mille billions, etc. Muni de cette convention, rappelons le carré magique donné dans l’article :

Sa constante magique vaut 141600 141600 141600 141600 291351. En remplaçant chaque nombre par son nom en toutes lettres on obtient :

Le nombre de lettres dans chaque case (on compte uniquement les lettres, pas les espaces ni les traits d’union) fournit un nouveau carré magique dont la constante est 525 :

Le carré initial est donc alphamagique. Répétons maintenant l’opération sur ce nouveau carré en écrivant les nombres en toutes lettres :

Puis comptons le nombre de lettres dans chaque case :

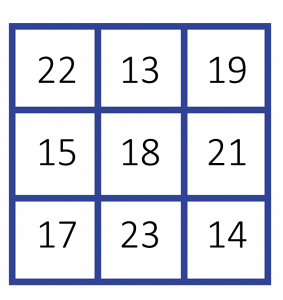
Ce carré est également magique, avec une constante de 54. Ceci établit que le carré de départ est doublement alphamagique.

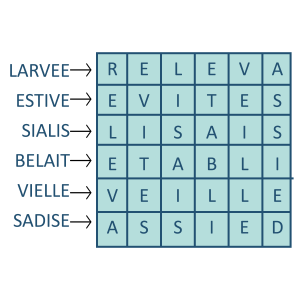
Carré magique de lettres

Les lettres, remises dans le bon ordre, forment une grille dans laquelle on retrouve les mêmes mots horizontalement et verticalement.