La gravure Melencolia du peintre allemand Albrecht Dürer (1471-1528) comporte de nombreux symboles mystiques qui ont donné lieu à d’innombrables interprétations : un compas, une balance, un sablier, etc. Celui qui nous intéresse ici est le carré magique dessiné sur le mur derrière l’ange, et reproduit aux côtés de la gravure ci-dessous. Pourquoi magique ?

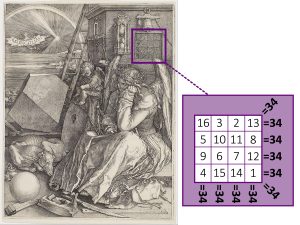
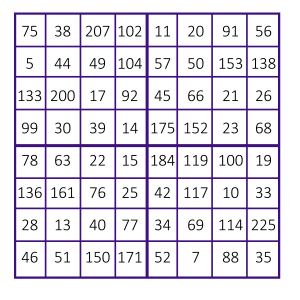
À cause de la façon dont les entiers de 1 à 16 sont disposés dans ses seize cases. Additionnez les quatre nombres de n’importe quelle ligne horizontale ou verticale, ou encore de l’une des deux diagonales : vous trouverez toujours la même somme, 34.

Étonnant, non ? En tout cas, suffisamment pour que les mathématiciens aient décidé d’appeler « magique » un carré qui a cette propriété. Mais celui-ci va beaucoup plus loin, on retrouve la somme de 34 de plusieurs dizaines de façons différentes : en additionnant les quatre coins, ou les quatre cases centrales, ou quatre cases formant un losange comme 4, 7, 13, 10, et bien d’autres.

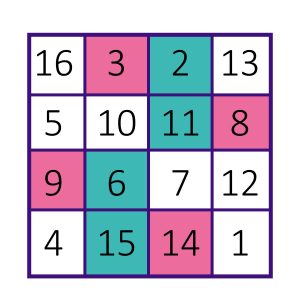
Une partie de la magie s’explique facilement si on remarque que les cases symétriques par rapport au centre ont toujours pour somme 17 — regardez comment sont placées les cases 1 et 16, 2 et 15, 3 et 14… N’importe quel motif de 4 cases symétrique par rapport au centre a donc pour somme 2×17 = 34, comme on le voit figure 3.

Cependant cela n’explique pas tout puisqu’on retrouve le même 34 dans des ensembles qui n’ont pas cette symétrie, par exemple les petits carrés formés par un coin et les trois cases qui l’entourent. Et la cerise sur le gâteau : les deux cases du milieu de la dernière ligne indiquent la date du tableau, 1514 ! Magique, on vous dit…

Les carrés magiques n’ont pas tous 16 cases, il en existe même de toutes les tailles. On peut remplir un carré d’ordre 3 (c’est-à-dire comportant 3×3 cases) avec les entiers de 1 à 9, aussi bien qu’un carré d’ordre 10 avec les entiers de 1 à 100, de façon que toutes les rangées, les colonnes et les diagonales aient la même somme. Toutes les tailles… ou presque ! on vérifie facilement qu’il n’existe pas de carré magique d’ordre 2, mais c’est la seule exception. Tous les carrés ayant la même taille ont la même « constante magique » (la somme que l’on retrouve sur toutes les lignes). Pour un carré d’ordre 4 la constante vaut 34 comme on l’a vu chez Dürer, pour l’ordre 3 la constante vaut 15, pour l’ordre 10 elle vaut 505… La formule générale est expliquée ici.

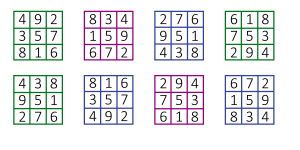
Combien y a-t-il de carrés magiques d’un ordre donné ? La réponse est en général… beaucoup ! Quand on a un carré magique, on peut immédiatement en trouver 7 autres par des symétries et des rotations, mais ils ne sont pas considérés comme réellement différents. Selon ce critère, il n’existe qu’un seul carré magique d’ordre 3, même s’il peut se présenter de 8 façons (figure 4). Une légende chinoise raconte que ce carré fut découvert sur la carapace d’une tortue sortie de la rivière Luo durant une inondation.

Pour l’ordre 4, au XVIIe siècle le mathématicien français Bernard Frénicle de Bessy a énuméré les 880 carrés réellement différents. Il faut ensuite attendre 1973 pour que l’Américain Richard Schroeppel dénombre les 275 305 224 carrés magiques d’ordre 5. Au-delà, le calcul reste à faire ; on sait tout de même grâce à une estimation de K. Pinn et C. Wieczerkowski en 1998 que pour l’ordre 6 c’est environ 17 milliards de milliards.

Nous avons dit qu’un carré magique contient des entiers successifs à partir de 1, mais rien n’empêche d’élargir la définition : on peut décider de considérer comme magique un carré de nombres quelconques, pas forcément consécutifs, dont la somme est la même sur toutes les rangées, les colonnes et les diagonales. À condition tout de même que les nombres soient tous différents, sinon c’est trop facile. La liberté supplémentaire que donne cette nouvelle définition permet de se poser de nouvelles questions. Par exemple, saurez-vous construire un carré magique d’ordre 3 contenant uniquement des nombres premiers (des nombres qui n’ont pas de diviseurs propres, comme 2, 3, 5, 7, 11, 13, 17…) ? Pour vous aider, sachez que la constante magique d’un tel carré vaut au minimum 177. Une solution se trouve sur le site de Pssst. Autre voie de recherche, les carrés magiques multiplicatifs, où ce n’est plus la somme mais le produit des nombres qui doit être le même sur toutes les lignes. Encore plus fort, le carré de la figure 5, découvert en 2005 par Christian Boyer, est doublement magique, à la fois par addition et par multiplication.

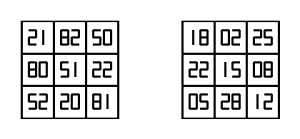
Les questions soulevées par les carrés magiques débordent parfois le cadre strict des mathématiques. On peut par exemple chercher un carré qui reste magique quand on le regarde la tête en bas. Cela suppose qu’on l’écrive avec une police de caractères dans laquelle certains chiffres restent lisibles quand on les retourne. Avec uniquement les chiffres 2, 5 et 8, saurez-vous construire un carré d’ordre 3 composé de nombres à deux chiffres, de constante 165, qui reste magique avec la même constante quand on le retourne (solution sur le site). Si on veut un carré qui reste magique mais avec une constante différente une fois retourné, la seule solution pour un carré d’ordre 3 avec des nombres inférieurs à 100 est celle de la figure 6.

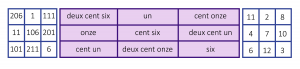
Puisque nous nous intéressons à la façon dont les nombres sont écrits, pourquoi ne pas aller un cran plus loin et les écrire en toutes lettres ? En 1986, l’ingénieur britannique Lee Sallows a proposé d’appeler « carré alphamagique » un carré magique tel que, si on écrit les nombres dans chaque case en anglais et qu’on compte les lettres utilisées, on obtient à nouveau un carré magique. Il existe de nombreux carrés alphamagiques en anglais et dans d’autres langues. La figure 7 montre le carré alphamagique français ayant la plus petite constante, 318.

En 2017 un autre britannique, l’informaticien Chris Patuzzo, a publié un carré doublement alphamagique : en remplaçant chaque nombre par le nombre de lettres de son nom en anglais, on obtient à nouveau un carré alphamagique. La figure 8 donne en exclusivité pour les lecteurs de Pssst le premier carré doublement alphamagique en français.

La vérification est un peu longue, vous la trouverez ici. À titre d’exemple, le nombre dans le coin supérieur gauche a un nom de 275 lettres : quatre-vingt-quatorze mille trois cent quatre-vingt-dix-neuf quadrillions quatre vingt-quatorze mille trois cent quatre-vingt-dix neuf trillions quatre-vingt-quatorze mille trois cent quatre-vingt-dix-neuf billions quatre-vingt quatorze mille trois cent quatre-vingt-dix-neuf millions quatre-vingt-dix-sept mille cent dix-sept.

Pour conclure, ayons une pensée pour les gens vraiment réfractaires aux mathématiques… En effet, certaines personnes baptisent « carré magique » un objet totalement différent, qu’on appelle plus couramment « mots carrés » : une grille de mots croisés, sans cases noires, dans laquelle les mots sont les mêmes horizontalement et verticalement, comme sur la figure 9. Avec les mots d’un dictionnaire usuel, y compris les verbes conjugués, on peut en trouver jusqu’à l’ordre 9.

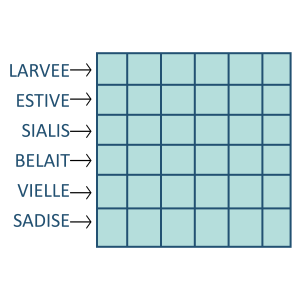
La figure 10 vous propose de remplir vous-même une grille d’ordre 6. Au lieu de définitions comme dans les mots croisés, les lettres de chaque mot de la grille vous sont données, réordonnées pour former d’autres mots. La solution se trouve sur le site de Pssst (Lien vers réponses).

Ce petit tour d’horizon n’a fait qu’effleurer le sujet des carrés magiques. Des livres entiers leur ont été consacrés, ainsi que d’innombrables sites web. Depuis les interprétations mystiques ou religieuses jusqu’à leur utilisation dans les tests d’engrais agricoles, en passant par les cubes magiques, voire les carrés géomagiques où les nombres sont remplacés par des formes géométriques, n’hésitez pas à partir à la découverte de ce monde merveilleux !